Kemajuan dalam teknologi perangkat keras dan lunak komputer saat ini menjadikan media digital sebagai media pilihan untuk penggambaran, pemetaan dan perhitungan cadangan. Bila gambar dan peta tersimpan dan tersajikan secara digital menggunakan paket-paket program terapan kelompok CAD ataupun GIS. maka hitungan panjang, luas dan volume dari satu gambar ataupun peta bisa diperoleh dengan mudah menggunakan program-program yang disediakan. Gambar yang dihitung luasnya bisa berupa gambar potongan, gambar kawasan yang dibatasi oleh garis kontur. Tahapan perhitungan cadangan dalam analisis geostatistik secara umum meliputi; pengamatan data lapangan, variografi, dan perhitungan variansi perkiraan dan variansi krigging.
Geostatistik Adalah ilmu yang mempelajaria aplikasi dan teori mengenai variabel terregional (variabel berubah) pada berbagai fenomena gejala alam, terutama untuk menentukan volume bahan galian. Landasan dari pembelajaran geostatistik adalah "The Theory of Regionaliset variables" dimana data dari titik-titik sample mempunyai korelasi satu sama lain sesuai dengan karakteristik penyebarab endapan mineral
Baca Juga : Analisa Produktivitas Peledakan Untuk Mencapai Target Produksi Peledakan,
Metoda Perhitungan Sumberdaya cadangan
Baca Juga : Analisa Produktivitas Peledakan Untuk Mencapai Target Produksi Peledakan,
Metoda Perhitungan Sumberdaya cadangan
Perhitungan Cadangan Dengan Geostatistik : Perhitungan Luas
Perhitungan Luas Cara Analitis
Bentuk Dasar Beraturan
1. Persegi empat; Bila panjang persegi empat P dan lebar L, maka luasnya LPE= P x L
2. Segitiga :
- Bila panjang satu sisi b dan tinggi segitiga pada sisi itu = h, maka luas segitiga LST = 1/2 bh.
- Bila sudut a diketahui dan sisi pengapitnya b dan c diketahui, maka luas segitiga LST = 1/2 bc sin a.
- Bila ketiga sisi segitiga masing-masing a, b, dan c diketahui, maka luas segitiga LST = (s(s - a)(s-b)(s-c))¹/² dengan s = 1/2 (a+b+c).
Hasil bentukan dari bentuk dasar beraturan
1. Bentuk turunan trapesium :
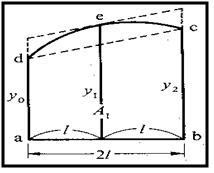
- Cara offset dengan interval tidak tetap : A = 1/2(S₁ y₁ +S₂ y₂ + S₃y₃ + .... + Sn yn ) dengan S₁ = d₁, S₂ = d₁ + d₂, S₃ = d₂ + d₃, S₄ = d₃ + d₄ dan S₅ = d₄
Gambar : Hitungan luas cara offset dengan interval tidak tetap
- Cara offset dengan interval tetap : A = d {(y₁ + y₂)/² + y₂ + y₃ + ... + yn-₁} dengan d adalah interval yang sama. pada gambar diatas, d₁ = d₂ = d₃ = d₄ = d. cara offset A = l (h₁ + h₂ + h₃ + ... + hn) = i S hi. dengan i = 1 ... n
Gambar. Hitungan luas cara offset pus
- Cara simpson 1/3. dua bagian dianggap satu set A = //3 ( y₀ + 4y₁ + y₂)
Gambar. Hitungan luas cara simpson 1/3 - Cara simpson 1/3 untuk offset ganda berulang A = //3 {y₀ + yn + 4(y₂ + y₄ + ... + yn-₁) + 2 (y₃ + y₅ + ... + yn-₂)}
- Bila koordinat (X,Y) suatu segi banyak diketahui, maka luasnya adalah A = 1/2 S X (Y₊₁ - Y𝘪-₁) atau A = 1/2 S Y₁(Xı-₁ - Xi-₁)
Gambar. Hitungan luas cara koordinat
Luas dihitung menggunakan rumus "typical" pada bentuk yang beraturan tersebut.
Contoh : Luas galian pada potongan yang ditunjukan pada gambar berikut adalah A = h(W + r₁h)
 |
| Gambar. Luas galian pada bentuk tanah asli beraturan |
5. Bentuk tanah asli tidak beraturan
Hitungan luas berdasarkan potongan lintang pada bentuk tanah asli tidak beraturan menggunakan cara koordinat. Koordinat perpotongan typical cross section dengan tanah asli harus dihitung.
Perhitungan Luas Cara Grafis
1. Cara kisi-kisi : bagian yang akan ditentukan luasnya "dirajah" dengan menempatkan kisi-kisi transparan dengan ukuran tertentu di atasnya. Luas = jumlah kelipatan kisi-kisi satuan.
 |
| Gambar. Hitungan luas cara kisi-kisi |
2. Cara lajur : bagian yang akan ditentukan luasnya " dirajah" dengan menempatkan lajur-lajur transparan dengan ukuran tertentu diatasnya. Luas setiap lajur = dl, bila d adalah lebar lajur dan l panjang lajur.
 |
| Gambar. Hitungan luas cara grafis lajur |
Perhitungan Luas Cara Mekanis - Grafis
Luas gambar diukur dengan menelusuri batas tepinya menggunakan pelacak pada alat planimeter. Luas kawasan yang diukur diperoleh dengan mengalikan bacaan manual luas planimeter dikalikan dengan skala gambar pada planimeter digital. bacaan luas planimeter secara digital direkam dan disajikan langsung oleh alat.
Perhitungan Cadangan : Volume
1. Cara Potongan melintang rata-rata : Bila A₁ dan A₂ merupakan luas dua buah penampang yang berjaraj L, maka volume yang dibatasi oleh kedua penampang ini V = 1/2 (A₁ + A₂) L
 | |
| Gambar. Volume cara potongan melintang rata-rata |
2. Cara jarak rata-rata dari penampang : V = 1/2(L₁ + L₂) A₀
 |
| Gambar. Volume cara jarak rata-rata |
3. Cara Prisma dan Piramida Kotak
- Cara prisma : V =h /6(A₁ + 4 Am + A₂)
Gambar. Volume cara prisma - Cara piramida kotak V = h/3{A₁ +(A₁A₂)¹/² +A₂}
Gambar. Volume cara piramida kotak
- Cara dasar ketinggian sama areal bujur sangkar, V = A/4(h₁ + 2 S h₂ + 3 S h₃ + 4 S h₄) h₁ = ketinggian titik-titik yang digunakan i kali dalam hitungan volume.
Contoh lihat XYZ. Titik-titik berurutan dari pojok kiri atas ke kanan terus ke bawah masing-masing digunakan dalam hitungan bujur sangkar : 1, 2, 2, 2, 1; 2, 4, 4, 3, 1 dan 1, 2, 2, 1 kali. contoh hitungan (Volume tinggi sama basis bujur sangkar).
Gambar. Volume cara dasar sama - bujur sangkar - Cara dasar ketinggian sama areal segitiga ; V = A/3(h₁ + 2S h₂ + 3S h₃ + 4S h₄ + 5S h₅ + 6S h₆ + 7S h₇ + 8S h₈) h₁= ketinggian titik-titik yang digunakan i kali dalam hitungan volume. Pelaksanaan hitungan menggunakan cara sama dengan cara bujur sangkar.
Gambar. Volume cara dasar sama - segitiga
 |
| Gambar. Volume cara kontur |
⥤ Cara garis kontur dengan rumus prisma
V = h/3{A₀ + An + 4SA₂𝑟+₁ + 2SA₂𝑟 }
𝑟 pada 2𝑟+1 berselang 0 ⇐ 𝑟 ⇐ 1/2 (n-2)
𝑟 pada 2𝑟 berselang 0 ⇐ 𝑟 ⇐1/2 (n-2)
Untuk n =2 diperoleh 𝑟 = 0, sehingga V = h/3(A₀ + A₂ + 4A₁) = h/3(A₀ + 4A₁ + A₂)
Bila n adalah ganjil, bagian yang terakhir dihitung dengan cara piramida kotak atau cara rerata luas penampang awal dan akhir.
⥤ Cara garis kontur rumus piramida kotak ;
V = h/3{A₀ + An 2SA𝑟 + S(A𝑟-₁ A𝑟) ¹/² }
r pada 2SAr berselang 1≤ r ≤ n - 1
r pada S (Ar - 1Ar)1/2 berselang 1≤ r ≤ n
Untuk n = 1 diperoleh V = h/3 {A₀ + A₁ + (A₀ A₁)₁/₂}
V = h/3 {A₀ + (A₀ A₁)1/2 + A₁}
Cara garis kontur dengan luas rata-rata ; V = h/2 {Ao + An + 2S Ar}
r bernilai 1 ≤ r ≤ n -1
Untuk n = 1 diperoleh V = h/2 ( A₀ + A₁)
Geostatistik (Statika Spasial)
Geostatistik merupakan cabang dari pada statistik terapan yang dibantu dengan deskripsi matematik dan analisa (observasi) geologi. Pada dasarnya statistik dapat digunakan untuk estimasi dan penelaahan variabel, faktor atau keadaan yang ada kaitanya dengan ilmu kebumian.
Variogram atau semivariogram merupakan alat utama dalam perhitungan melalui geostatistik, selain itu dapat juga untuk mengukur variansi (mean squarred error) dalam estimasi nilai Z(x+h) dengan Z(x), jika sampel pada posisi x+h nilainya sama dengan sampel pada posisi x, maka kesalahan adalah Z(x) - Z(x+h), yang kuadrat rata-ratanya bernilai 2ɣ(h). Persamaan Semivariogram eksperimental adalah :
Model variogram eksperimental yaitu variogram yang diperoleh dengan memasukan nilai sampel dalam rumus variogram merupakan realisasi dari pada sifat-sifat spasial dari regionalized variabel. Hal ini dilakukan agar variogram tersebut dapat digunakan untuk alat estimasi nilai suatu dimensi yang lebih besar dari pada ukuran sampel sehingga perlu adanya model teoritis yang cocok dengan realisasi sifat-sifat spasial berkaitan dengan regionalizad variabel yang sedikit memperlihatkan keadaan statis.
Variogram yaitu representasi hubungan antar data secara spasial (ruang) pada suatu arah tertentu. Dimana dapat dirumuskan dalam rumus umum dibawah ini :
Dimana :
𝜸(h) : Nilai variogram untuk arah tertentu dan jarak h
h : 1d, 2d, 3d, 4d, (d = jarak k antara conto)
z(x₁) : harga (data) pada titik x₁
z(x₁+h) : data pada titik yang berjarak h dari xi
N(h) : Jumlah pasangan data
Metode seperjarak (Invers Distance Method)
Metode matematik banyak diterapkan pada tahap awal evaluasi mineral deposit. Metode dan teknik perhitungan dipengaruhi oleh kondisi geologi lokal, metode penambangan dan lain sebagainya. Metode yang diterapkan, dalam praktek yang sebenarnya selalu sesuai dengan teori yang diberikan. Salah satu metode perhitungan tersebut adalah metode Invers Distance.
Prinsip penaksiran metode Invers Distance adalah dilakukan teknik pembobotan titik data yang didasarkan pada :
- Letak grid atau blok yang akan ditaksir terhadap letak data conto
- Kecenderungan Penyebaran data kualitas
- Orientasi setiap conto yang menunjukan hubungan letak ruang antar conto
Pemecahan masalah pada metode bijih ini dengan metode dengan didasari pada jarak sample lainya pada satu blok. Umumnya pembobotan jarak dengan metode menurut sample yang ditampilkan dengan cara penerapanya :
- Invers distance
- invers distance squared
- Invers distance cubed
➣ Invers distance squared
Persamaan pembobotanya
Faktor pembobotan
➣ Invers distance cubed
Persamaan pembobotanya
Faktor pembobotan
Perincianya adalah sebagai berikut :
➫ sudut perubah yang maksimum
➫Dimensi ruang sesuai dengan pola penyelidikan yaitu :
- Square
- Circle
- Rectangle
- Ellips
➫ Jika titik sample nyatanya terdapat pada tengah-tengah blok maka diperkirakan keadaan ini d = 0, menyebabkan nilai d kecil yaitu 1m.
➫Hal yang mencirikan titik minimum dalam ruang maka diijinkan untuk melakukan interpolasi
➫Jika jumlah titik tersebut tidak cukup memadai maka penyelidikanya diperluas hingga jumlahnya cukup memadai ruang tersebut. Contoh untuk perluasan bentuk rectangle dalam perluasan 25% panjang dan lebar.
Pada metoda invers distance :
- Memperhitungkan adanya hubungan letak ruang (jarak)
- Merupakan kombinasi linear atau harga rata-rata tertimbang (weighting average) dari titik-titik data yang ada disekitarnya.
- Pada titik data yang terdekat dengan titik yang ditaksir akan memberikan bobot yang lebih besar dari pad titik data yang lebih jauh.
- Efek penghalusan (pemerataan) dilakukan dengan faktor pangkat
- Pada pangkat yang sangat besar akan menghasilkan pendekatan metode poligon.
- Pangkat semakin besar maka bobot (pengaruh) dari titik terdekat semakin besar pula.
Kelemahan
- Tidak ada hubungan antara jarak dan range a pada variogram
- Pada deposit irregular dengan range kecil akan diperlakukan sama dengan pada deposit reguler dengan luas a.
- Jika titik referensi adalah lubang bor, kemudian faktor pembobotan tak berhingga, maka metoda ini tidak dapat diterapkan.
- Metoda ini didasarkan pada estimasi titik dan tidak bergantung pada ukuran blok.
- Invers distance hanya memperhatikan jarak dan belum memperhatikan efek pengelompokan data.
- Sehingga data dengan jarak yang sama namun mempunyai pola sebaran yang berbeda masih akan memberikan hasil yang sama.
- Metoda ini belum memberikan korelasi ruang antara titik data dengan titik data yang lain.
Krigging yaitu suatu teknik perhitungan untuk estimasi dari suatu variabel terregional (regionalized variable) yang memakai pendekatan bahwa data yang dianalisis dianggap sebagai suatu realisasi dari suatu variabel acak (random variable),dan keseluruhan variable acak dalam daerah yang dianalisis tersebut akan membentuk suatu fungsi acak dengan menggunakan model struktural variogram (Dr.Ir. Rukmana Nugraha Adhi, 1998).
Krigging adalah penaksiran geostatistik linier tak bias yang paling bagus untuk mengestimasi kadar blok karena menghasilkan varians estimasi minimum → BLUE (Best Linier Unbiased Estimator) (DR. Ir. Totok Darijanto, 2003). krigging diambil dari nama seorang pakar geostatistik dari Afrika Selatan yaitu D.G Krige yang telah banyak memikirkan hal tersebut sejak tahun 50an.
Secara sederhana krigging menghasilkan bobot sesuai dengan geometri dan sifat mineralisasi yang dinyatakan dalam variogram. Bobot yang diperoleh dari persamaan krigging tidak ada hubunganya secara langsung dengan kadar conto yang digunakan dalam penaksiran. Bobot ini hanya tergantung pada konfigurasi conto disekitar blok serta model variogramnya.
Nilai estimasi (1) dan variabel estimasi krigging (2) yang ditentukan dengan metoda geostatistik untuk suatu variabel terregional disetiap support V adalah sebagai berikut
a) Blok teratur
b) Blok tidak teratur
 |
| Gambar. Perhitungan metoda geostatistik dengan support suatu blok |
Dan ai ditentukan dariperkalian matrik pada persamaan kriging (3,4,5,6) persamaan kriging (3)
Dari persamaan krigin tersebut, menjadi perkalian matrik sebagai berikut :
Perhitungan dengan metoda krigging ini kadang-kadang terlalu komplek untuk suatu komoditi tertentu. Hal ini sangat bermanfaat jika dilakukan pada penentuan cadangan-cadangan yang mineable dengan kadar-kadar diatas cut iff grade.
Sebagai contoh hubungan antara analisa conto dengan harga analisa blok bijih (harga sebenarnya) yang tetpencar membentuk elips (gambar dibawah) kemudian tarik garis regresi memalui titik 0 dan titik (Ž,ž), selanjutnya bagi elips tersebut dengan cut off grade zc = Zc = 5% menjadi empat bagian
 |
| Gambar, Pencaran data antara conto vs kadar blok yang memperlihatkan kesalahan penambangan |
Daerah 2 Semua blok dengan kadar < cog yang sesuai dengan kadar conto < cog ditambang
Daerah 3 Semua blok dengan kadar < cog yang sesuai dengan kadar conto > cog ditambang
Daerah 4 Semua blok dengan kadar > cog yang sesuai dengan kadar conto < cog ditambang
Jika garis regresi B _ B' yang menunjukan hubungan antara conto dan kadar blok diplot, maka blok - blok dengan kadar 5% juga akan ditambang walaupun kadar conto kadar 3,5% (gambar atas). Daerah 4 pada gambar 1 yang baik ditambang karena kesalahan informasi menjadi kecil, sementara itu daerah 3 yang ditambang walaupun berkadar rendah menjadi lebih besar, walaupun demikian secara keseluruhan daerah dengan blok-blok yang mempunyai kadar > cut off grade (5%) dan ditambang menjadi lebih besar.
Berdasarkan analisis variogram, Mathero memberikan koreksiperkiraan kadar pada suatu blok yang tidak hanya dipengaruhi oleh conto didalam blok saja, tetapi juga pada conto-conto disekitarnya.
 | |
| Gambar. Perubahan bentuk elips pencaran data akibet koreksi dengan metoda kriging |
Metoda Perhitungan Cadangan Batubara
Metoda penampang (cross-section) masih sering dilakukan pada tahap awal. Penaksiran secara manualini dipakai sebagai pembanding untuk mengecek hasil sebagai penaksiran menggunakan komputer. Rumus yang dapat digunakan dalam perhitungan luas rata-rata (mean area) dipakai untuk endapan yang mempunyai penampang yang uniform.
Rumus Mean area
V = L (S₁+S₂)
2
Dimana
S₁ : Luas penampang 1
S₂ : Luas penampang 2
L : Jarak antar penampang
V : Volume cadangan
Dimana
S₁ : Luas penampang 1
S₂ : Luas penampang 2
L : Jarak antar penampang
V : Volume cadangan
Rumus Prismoidal
V = (S₁ +4M +S₂ )
6
Dimana
S₁ S₂ : Luas penampang 1&2
M : Luas penampang tengah
L : Jarak antar penampang S₁ dan S₂
V : Volume cadangan
Sumber :
Perhitungan cadangan dan geostatistik Dudi Nasrudin Usman, S.T
Dimana
S₁ S₂ : Luas penampang 1&2
M : Luas penampang tengah
L : Jarak antar penampang S₁ dan S₂
V : Volume cadangan
Sumber :
Perhitungan cadangan dan geostatistik Dudi Nasrudin Usman, S.T
Posting Komentar untuk "Perhitungan Cadangan Dengan Geostatistik dan kriging"